	Sign In Sign-Up

Bernoulli Hoverdisk

The Bernoulli hover disk operates on the Bernoulli principle, creating a pressure differential between the top surface of a rotating disk and the bottom surface of a stationary plate, while keeping the interior surfaces both near zero pressure.

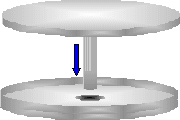The disk is on a bearing axle, which penetrates the plate and comes out on the other side. This axle serves both as a driveshaft for a motor to spin the disk, and as a load bearing element, to reduce the amount of force on the seal at the rim. Properly engineered, the bearing axle should take enough of the force to make the force on the rim almost negligible.

This picture illustrates the approximate appearance of the assembled unit, without any mounting or motor. The unit would be mounted by securing the base plate directly to the same carriage as the motor, and the motor being mounted so as to turn the drive shaft protruding though the baseplate of the unit.

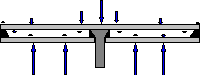In this cross sectional illustration, you can see the main elements of the hoverdisk. The blue arrows are a representation of atmospheric pressures acting on the various parts of the disk. The black portions are representative of a hermetic seal, of some material that is both resilient and slick, which can take advanced lubrication. Silicone is one possibility. The space in between the plates is a vacuum, and is denoted by the very small arrows to indicate atmospheric pressure. The bottom of the stationary baseplate will be under full atmospheric pressure, and the top will be spinning, thus having lower pressure out near the rim, where the higher velocity of the surface will produce a relatively more significant effect, and full atmospheric pressure in the center, which will be turning but not moving at high speed.

Bernoulli's equation can be formed as follows:

P + dgh + ½dv² = P' + dgh' + ½dv'²

where P, h, and v represent the pressure, height, and velocity of one point in a liquid, and P', h', and v' represent the pressure, height, and velocity of another point in a liquid. If we take one of these points to be a point of the atmosphere in contact with the spinning surface of the disk, and the other to be some point in contact with the stationary base, then we can simplify the equation as follows:

P + ½dv² = P' + ½dv'²

because although there is a height difference, which contributes to the natural buoyancy of any solid in air or another liquid of non zero density, the difference is so small as to be negligible, barely more than one pascal per meter of height difference. Further, since the base plate is stationary, we may also identify the term v' as zero, and thus reduce the part of the equation multiplied by v to zero, producing the following:

P' + ½dv'² = P

then we subtract ½dv² from both sides:

P' = P - ½dv'²

Which demonstrates that the pressure at any point on the spinning surface of the disk is at atmospheric pressure, less the quantity produced by ½dv², where v is the velocity of the surface of the disk and d is the density of air.

Calculating the value of the force imbalance created by this pressure reduction involves the following. First, we take the pressure imbalance at the rim of the disk as being equal to P, and the radius of the disk as being r, and K being a constant with the dimensions of 1/t, where t is some time, then we may relate this to the velocity of the edge of the disk as follows:

½dv² = P, v = rK

And let us say that the velocity of any other point on the surface of the disk at a lesser radius r' will be v', and the pressure imbalance will be P'. The following statements are also true.

½dv'² = P', v' = r'K

K being the same constant as found in the previous instance. Thus by substitution:

½dK² r'² = P'

Because we already assume that v and r were givens, this leaves a direct relation between r'² and P'. Now we must turn to relating P' to a unit of area, so as to produce a force. The equation for the area A of the disk is simple:

A = pr²

of course, this is equal to the integral of the circumference C' at r'

C' = 2pr'

Thus, we can multiply this equation by the equation for P', and get the following:

P' C' = 2pr' ½dK² r'²

or P' C' = pdK² r'³

which integrates to F = 1/4pdK² r²² = 1/4pdv² r² = 1/2pP r²

And thus you can see that the pressure differential at the rim, times one half, times the area of the disk, gives the total force. I know that the math needs polishing, but I think it's basically valid. Anyway, the concept is basically valid, and that means that the rest is engineering. The more important equation is there in the middle, one quarter of the density times the velocity squared times the area of the disk is more practical in terms of what is needed for the critical tolerances. It means that a disk with a radius of one meter turning at couple of hundred rpm should produce over four hundred newtons of lift. Twice the speed would produce four times as much lift, up to a limit that is reached once the disk is turning somewhere over a thousand rpm. Of course, in water the numbers are all very different, as is the design that you want to work with. But I'm sure that you can work that out for yourself. In fact, if you could clean up any...umm, unintelligible spots in the math, that would be good. I'm acting mostly on instinct for much of it. I really need to find some of my books and review all that stuff. I'm sure that I made it all overly complicated. And if you decide to build one, be sure and send me a picture! Just kidding. I can think of a gazillion cool things to do with these, though. A flying house is just the one I'm fondest of.